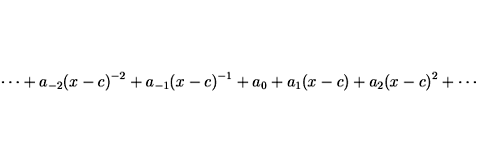We are moving toward what one scholar, Bertram Grass, calls “friendly fascism.” ...When the difference between lies and the truth no longer means anything, we become easy to manipulate-fair game for “mass media, world spanning corporations, armies and intelligence agencies,” he wrote. “Meanwhile, the majority of people have little part in the decisions that affect their families, workplaces, schools, neighborhoods, towns, cities, country, and the world.”
—Jonathan Vankin, Conspiracies, Cover-ups, and Crimes: Political Manipulation and Mind Control in America.
At one time, when I was still young, I had a very optimistic view of the world. I believed everything could be understood through logical deduction. Cause and effect was a basic rule which permeated everything from science to society. Society itself was an organism with natural rhythms which governed the way it adapted and grew. Mathematics was God.
I saw Mathematics as this pervasive entity behind all things which had a simplicity that I equated with elegance. In a system where 1 + 1 always equals 2, it was easy to talk about Truth and Order. Elementary arithmetic was a face given to the undeniable laws of the universe, which have existed forever with no beginning and no end. These were self-evident truths. When I was a sophomore in high school, there was a white-haired boy-genius in my Trigonometry class—a freshman, who mocked these truths. He came into class one day and started talking about how he knew that 1 + .999999... (repeating forever) is equal to 2 in the same way that 1 + 1 is equal to 2. This seemed impossible. How could two different pairs of numbers be added up and equal the same thing? I couldn't accept it and threw a fit. I screamed that the number 2 could not be equal to 1 + .999999... if it was already equal to 1 + 1. We argued for hours until
It wasn't such a tight system after all, maybe not worthy of being worshiped.
Around the same time while I was in high school, the U.S. invaded Iraq during the Gulf War. I had never been politically aware or really cared up until then. All I could understand was that the government had gotten us involved in a war and we were fighting it. As an awkward looking, skinny teenager I had my own problems to worry about. One day, a group of students felt that it was time for everyone to wake up and do something, so they got permission to hold a student walk out in peaceful protest of the war. And students did walk out of their classes, but it wasn't peaceful and it wasn't in protest. In America at that time there was a severe backlash against pacifism, anti-consumerism, and hippies in general. Although the Republicans controlled the White House, it wasn't as glamorous as the backlash in the Eighties. The American public just seemed to be turning out to be a bunch of rednecks. Rednecks had always been on campus at my high school, but they kept their hatred and ugliness to the side streets. That day they came out in herds and piled into their raised 4 wheel drive monster trucks and paraded huge American flags up and down the streets surrounding the school. Other students magically produced huge American flags and crossed the campus in a giant tidal wave which crashed down on the group of students who organized the protest, 2 screaming girls and a boy perched on the back stage of the drama department's theater. I didn't know those kids at the time. I was a homeboy and they were goths and hippie kids. Years later I joined their tribe, listened to their music, wore their combat boots, even fell in love with one of them, and then finally adopted their politics. As I trailed behind the wave of pro-war demonstrators with my friends, strutting and just listening and watching, as we always did, I had an unsettling feeling. Of course, we didn't care either way, but the way the protesters looked, so miserably small and sad, way down there as the wave engulfed and washed over them, seemed wrong. It didn't seem wrong that they were there, even though they were the only ones not holding on to the edge of some huge parachute-like American flag. What did seem wrong was that the rednecks in their trucks flying by were cheering us on. Even if I was at the tail end of the wave that was chanting "Support Our Troops" and putting on the biggest display of apathy, I was still following. In a moment of self awareness, I stepped out of myself and looked down on the crowd and wondered how many other people had actually thought about what they were doing and knew where the heck they were going with this giant American flag. I still can't shake the image of those fanatic rednecks standing in the back of a speeding truck, all of them reaching out to clutch the pole of an American flag.
Midway through college, I dropped out of the Physics program and, looking for something I could understand, I re-discovered mathematics. I signed up to be a Mathematician and discovered a world where classical thinking was already thoroughly deconstructed and where God didn't exist. Logical deduction, or "inductive reasoning," was even a myth. What I'd discovered was actually the legacy of postmodern mathematicians like Bertrand Russell and Kurt Gödel who's work in the early 20th century unseated basic theoretical structures like arithmetic and concepts like universal truth. In 1931, Kurt Gödel published a revolutionary paper called "On Formally Undecidable Propositions," in which he proved what is known as Gödel's Incompleteness Theorem. Gödel's proof shows the inconsistency of very large deductive systems like elementary arithmetic. He proved with a system so large and all-encompassing it's possible to formulate straightforward mathematical statements which can neither be proved nor disproved using the axioms of the system. The axioms, or so-called self-evident truths, would have to use reasoning added-on to iron out the inconsistencies to such a complex degree that the axioms themselves would--well, no longer really be self-evident and could be called into doubt. Gödel went further to prove for any consistent set of arithmetical axioms, there are true mathematical statements which cannot be derived from the set. New axioms can be added-on indefinitely but they will never encompass even more true statements which can be found. Elementary arithmetic and anything like it is essentially incomplete. When I discovered this proof, it was not only fodder for the fire of the discontent I was already feeling but justification. I proceeded to leave my apartment to return to a student co-op which I'd thought I'd grown out of, became a vegetarian, partook in many mind altering “experiments” and failed many of my classes. The world was suddenly much more malleable than I had originally perceived. While it was in my hands, I felt that I could do anything with it.
Even after I left college, I still liked to call myself optimistic--which at the time I thought was just out of irony. But looking back I really think it was sincere because I couldn't ignore my faith in Mathematics as the complex, unstable God she truly is. I had grown up and understood that logical deduction wasn't really all there was to understanding things. After Gödel's theorem, the self-evident Truths, the Principia, and my system of beliefs were shaken to the core. I could no longer rely on cause and effect, and evolution didn't make sense when talking about Society, Civilization or human behavior. I questioned the underlying processes without relying on logic, cause/effect or what should be "self-evident."
Today it's hard not to have a disenchanted world view. Democracy, it seems, by modern definition, is a system in which the governing body is, at times, required to ask the people—all at once—what must be done concerning some issue, or, concerning some person who will in turn make decisions about many issues. The mechanics behind asking all of the people at once appear to have become so cumbersome that it's not possible for the people to be sure or to verify what the government heard is what the they asked for. Many times not even they know what they were asking for. Political rhetoric, propaganda and outright fraud are part of a repertoire in an age-old system under which our apparent order operates. But do not doubt that even as it evolves and adapts, the people it's designed to govern have continued to increase their awareness and at times show substantial resistance. What kind of logic is behind the reasoning that has been keeping you in your chair, in your cubicle, on a day like today? Rise up.
Well there's no more sleepless nights for me
Now it's easier from now on
Because I've realised exactly where I've been going wrong
Well I've been lying awake at night
Worrying about the Russians
But the Russians are my friends
Because we've got a love that will never end
Because now I've learned to love the bomb
Now I've learned to love the bomb...
—Television Personalities, How I Learned to Love the Bomb